Research
Mathematical and Computational Biology
Analysis of single-cell and spatial omics data
Single-cell RNA sequencing (scRNA-seq) provides transcriptomic details of individual cells which reveals novel cell types and temporal trajectories of cells.
More challenging questions can be addressed when we pair scRNA-seq with other technologies or data resources supplying the missing information.
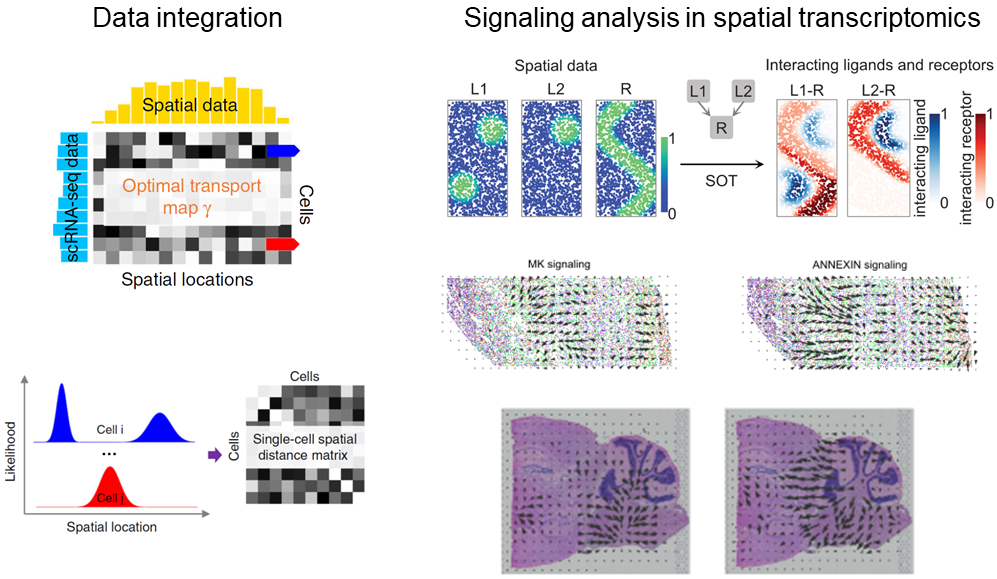
We are generally interested in integrating single-cell or spatial omics data and analyzing inferring complex processes from these data such as cell-cell communications.
For example, the missing spatial information of scRNA-seq data can be retained by integrating with spatial gene expression data.
With the spatially annotated scRNA-seq data or the recent spatial transcriptomics data, cell-cell communication, a process with a strong spatial limitation, can be studied in detail.
In both tasks, we use optimal transport and its variants motivated by the biological problems.
The datasets to be coupled or the spatial distribution of ligand or receptor expressions are viewed as distributions to be coupled.
The complex processes and relationships are better dissected by finding the globally optimal coupling plans.
Related works
- Cang, Zixuan, Yanxiang Zhao, Axel A. Almet, Adam Stabell, Raul Ramos, Maksim V. Plikus, Scott X. Atwood, and Qing Nie. "Screening cell-cell communication in spatial transcriptomics via collective optimal transport." Nature Methods (2023) DOI: https://doi.org/10.1038/s41592-022-01728-4
- Ren, Honglei, Benjamin L. Walker, Zixuan Cang, and Qing Nie. "Identifying multicellular spatiotemporal organization of cells with SpaceFlow." Nature communications 13, no. 1 (2022): 1-14.
- Cang, Zixuan and Qing Nie. "Inferring spatial and signaling relationships between cells from single cell transcriptomic data." Nature communications 11, no. 1 (2020): 1-13.
- Cang, Zixuan, Xinyi Ning, Annika Nie, Min Xu, and Jing Zhang. "Scan-IT: Domain segmentation of spatial transcriptomics images by graph neural network." In BMVC. (2021).
- Almet, Axel A., Zixuan Cang, Suoqin Jin, and Qing Nie. "The landscape of cell-cell communication through single-cell transcriptomics." Current opinion in systems biology 26 (2021): 12-23.
Predictive modeling of molecular structures
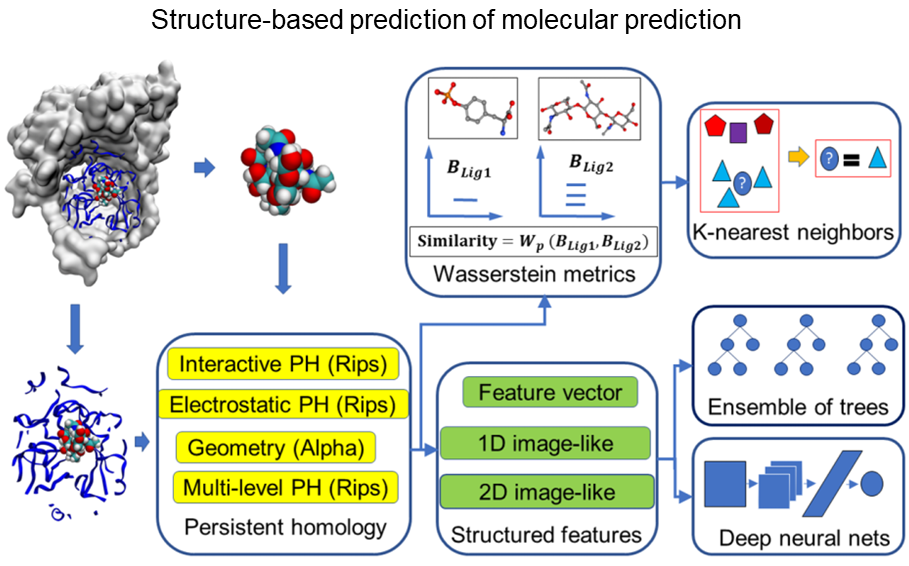
Computational predicting various properties of biomolecules is a key component in modern drug discovery workflow.
This is a challenging task due to 1) the structural complexity of macro-biomolecules and 2) the limited data resources of biomolecular properties.
We adapt topological data analysis to deriving concise structural representations of biomolecules so that machine learning models can be effectively trained with the small functional data.
This strategy has been shown to be very competitive in various applications, for example, in D3R challenges for computational drug discovery (see this report paper for the performance in one D3R challenge).
Related works
- Cang, Zixuan, and Guo-Wei Wei. "TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions." PLoS computational biology 13, no. 7 (2017): e1005690.
- Cang, Zixuan, Lin Mu, and Guo-Wei Wei. "Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening." PLoS computational biology 14, no. 1 (2018): e1005929.
- Cang, Zixuan, and Guo-Wei Wei. "Analysis and prediction of protein folding energy changes upon mutation by element specific persistent homology." Bioinformatics 33, no. 22 (2017): 3549-3557.
- Cang, Zixuan, and Guo‐Wei Wei. "Integration of element specific persistent homology and machine learning for protein‐ligand binding affinity prediction." International journal for numerical methods in biomedical engineering 34, no. 2 (2018): e2914.
- Zhao, Rundong, Zixuan Cang, Yiying Tong, and Guo-Wei Wei. "Protein pocket detection via convex hull surface evolution and associated Reeb graph." Bioinformatics 34, no. 17 (2018): i830-i837.
Data-driven modeling of biological systems
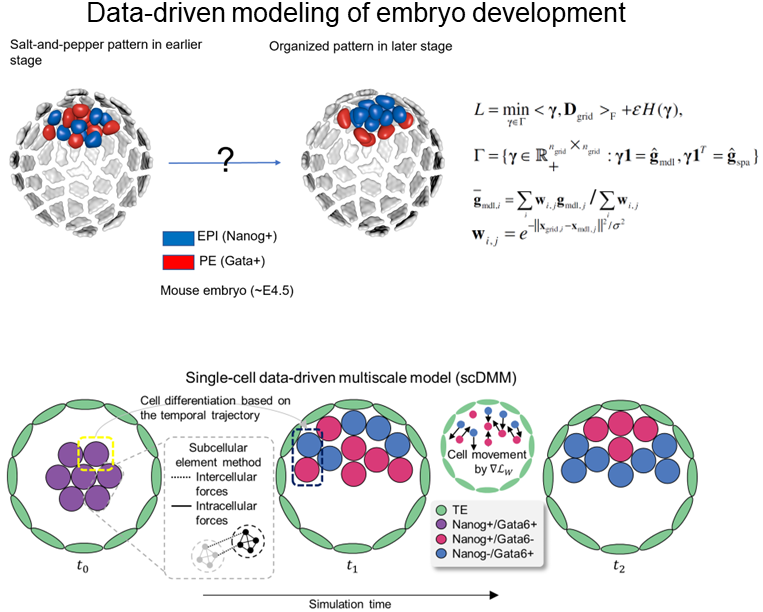
The various data resources provides an opportunity to incorporate data into mechanistic models to study complex biological systems.
Here as an example, we study the development of early mammalian embryo with the help of single-cell RNA sequencing and spatial gene expression data.
During early mammalian embryo development, a small number of cells make robust fate decisions at particular spatial locations in a tight time window to form inner cell mass (ICM), and later epiblast (Epi) and primitive endoderm (PE).
Here we build a multiscale three-dimensional model for mammalian embryo to recapitulate the observed patterning process from zygote to late blastocyst.
By integrating the spatiotemporal information reconstructed from multiple single-cell transcriptomic datasets, the data-informed modeling analysis suggests two major processes critical to the formation of Epi/PE layers: a selective cell-cell adhesion mechanism for fate-location coordination and a temporal attenuation mechanism of cell signaling.
Related works
- Cang, Zixuan, Yangyang Wang, Qixuan Wang, Ken WY Cho, William Holmes, and Qing Nie. "A multiscale model via single-cell transcriptomics reveals robust patterning mechanisms during early mammalian embryo development." PLoS computational biology 17, no. 3 (2021): e1008571.
Topological Data Analysis and Optimal Transport
Topological data analysis
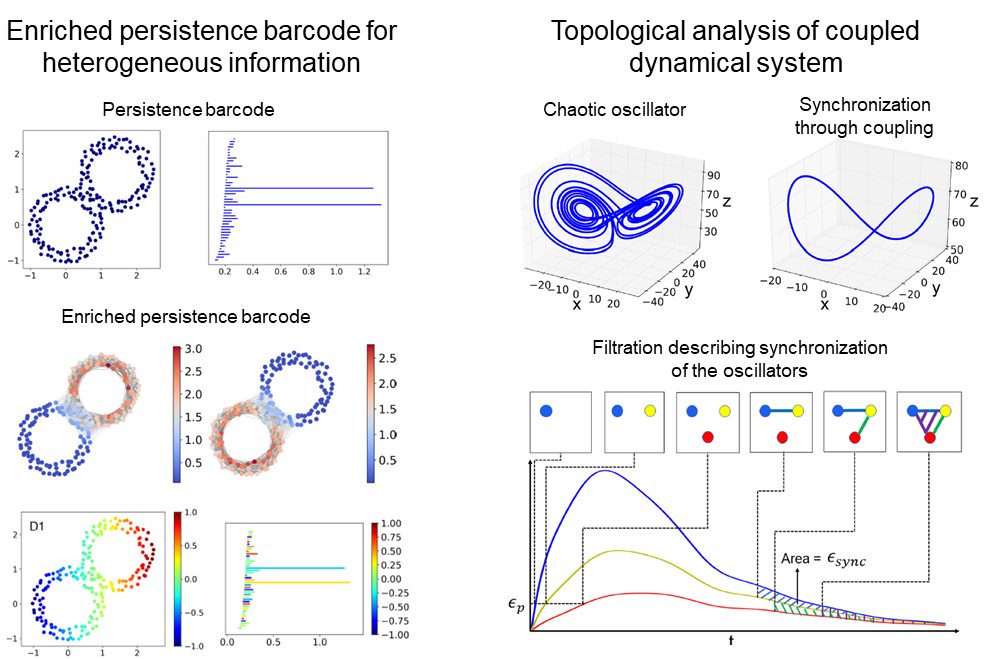
Topological data analysis is a powerful tool for describing complex and high-dimensional data and a major tool is persistent homology.
Motivated by the application to molecular structure analysis, we develop TDA methods suitable for the heterogeneous molecular descriptions.
Using persistent cohomology, we can connect the non-geometric information to the topological characterization of the geometric information so that both kinds of information are represented in the resulting enriched persistence barcodes.
We can also define filtrations to handle dynamics involved in molecular interactions.
Related works
- Cang, Zixuan, and Guo-Wei Wei. "Persistent cohomology for data with multicomponent heterogeneous information." SIAM Journal on Mathematics of Data Science 2, no. 2 (2020): 396-418.
- Cang, Zixuan, Elizabeth Munch, and Guo-Wei Wei. "Evolutionary homology on coupled dynamical systems with applications to protein flexibility analysis." Journal of Applied and Computational Topology 4, no. 4 (2020): 481-507.
Optimal transport
Optimal transport has gained tremendous attention due to its application in deep learning.
It is also an indispensable tool for finding correspondence between paired datasets and interactions among cells.
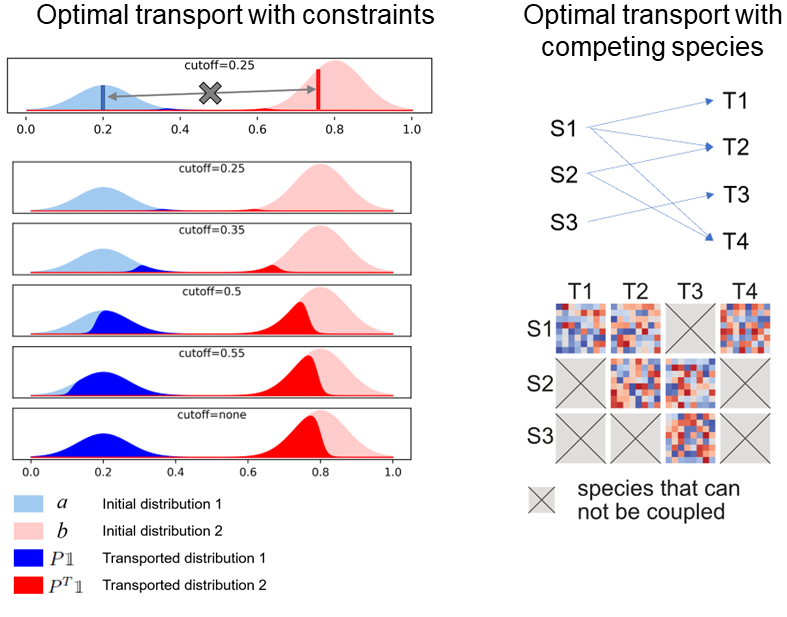
In the applications of optimal transport to integrating scRNA-seq and spatial data and inferring cell-cell communications, it is natural to enforce constraints such that dissimilar cells should not be connected in data integration and communication between cells that are too far away is unreasonable.
Motivated by this, we develop supervised optimal transport where the transport plan is restricted by application-induced constraints.
Related works
- Cang, Zixuan, Qing Nie, Yanxiang Zhao. "Supervised optimal transport." SIAM Journal on Applied Mathematics 82, no. 5 (2022): 1851-1877.